Table Of Content
For instance, if you had a plot of land the fertility of this land might change in both directions, North -- South and East -- West due to soil or moisture gradients. As we shall see, Latin squares can be used as much as the RCBD in industrial experimentation as well as other experiments. Second, the blocking variable cannot interact with the independent variable. In the example above, the cell phone use treatment (yes vs. no) cannot interact with driving experience.
Error
After calculating x, you could substitute the estimated data point and repeat your analysis. So you can analyze the resulting data, but now should reduce your error degrees of freedom by one. In any event, these are all approximate methods, i.e., using the best fitting or imputed point. Basic residual plots indicate that normality, constant variance assumptions are satisfied. Therefore, there seems to be no obvious problems with randomization. These plots provide more information about the constant variance assumption, and can reveal possible outliers.
The most dangerous block in Chicago, once home to Michelle Obama: 'O block' - Chicago Sun-Times
The most dangerous block in Chicago, once home to Michelle Obama: 'O block'.
Posted: Sun, 02 Nov 2014 07:00:00 GMT [source]
Graphic Design in Businesses
The only randomization would be choosing which of the three wafers with dosage 1 would go into furnace run 1, and similarly for the wafers with dosages 2, 3 and 4. An ANOVA table provides all the information an experimenter needs to (1) test hypotheses and (2) assess the magnitude of treatment effects. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Crossover Design Balanced for Carryover Effects
This is a Case 2 where the column factor, the cows are nested within the square, but the row factor, period, is the same across squares. Together, you can see that going down the columns every pairwise sequence occurs twice, AB, BC, CA, AC, BA, CB going down the columns. The combination of these two Latin squares gives us this additional level of balance in the design, than if we had simply taken the standard Latin square and duplicated it.
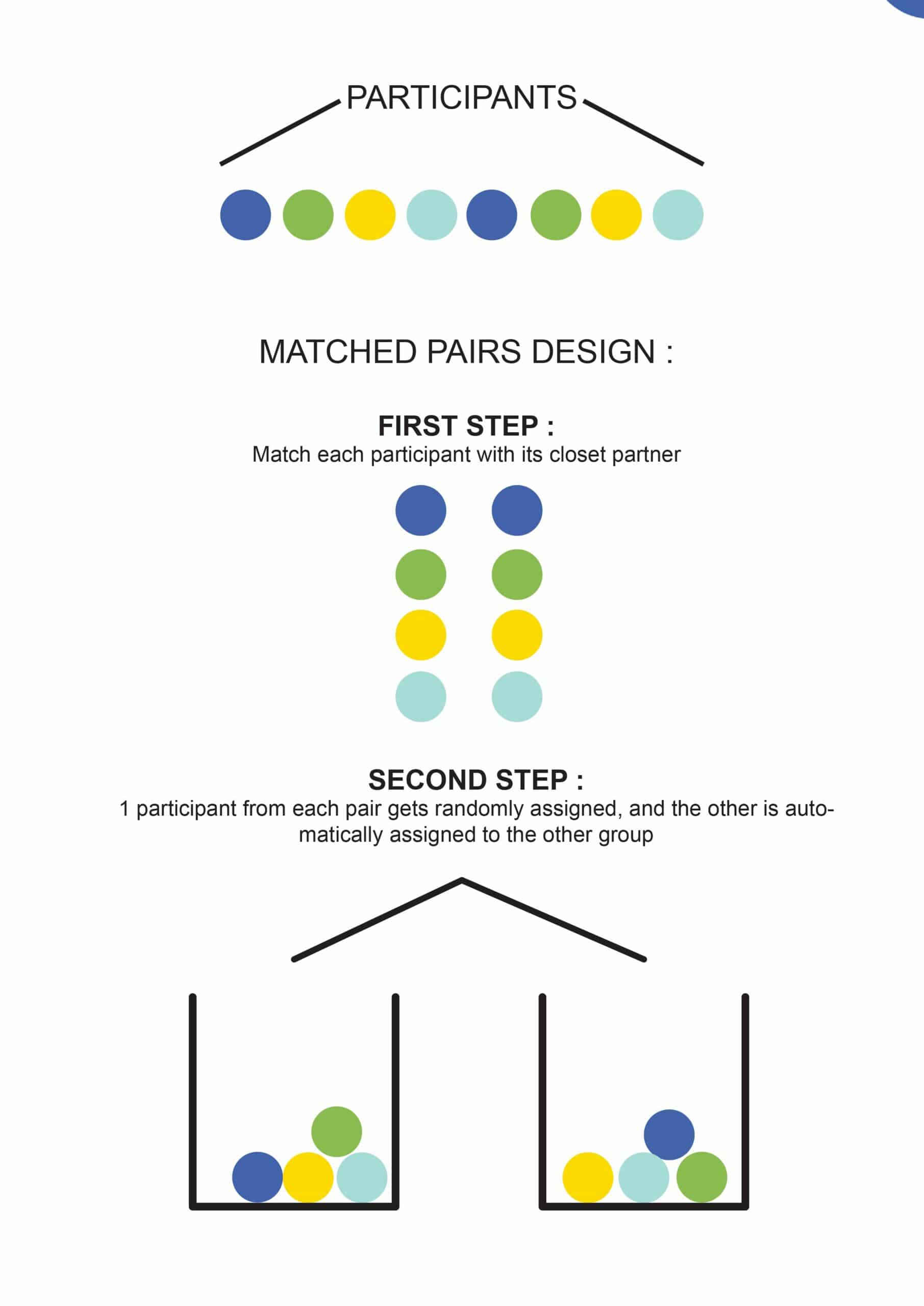
In a randomized complete block design (RCBD), each block is of the same size and is equal to the number of treatments (i.e. factor levels or factor level combinations). Furthermore, each treatment will be randomly assigned to exactly one experimental unit within every block. So we think of the data in the greenhouse example in terms of RCBD, we will have 6 blocks each with block size equal to 4, the number of fertilizer levels. A randomized block design is an experimental design where the experimental units are in groups called blocks. The treatments are randomly allocated to the experimental units inside each block. When all treatments appear at least once in each block, we have a completely randomized block design.
The great firewall of China: Xi Jinping’s internet shutdown - The Guardian
The great firewall of China: Xi Jinping’s internet shutdown.
Posted: Fri, 29 Jun 2018 07:00:00 GMT [source]
This subset of columns from the whole Latin Square creates a BIBD. With our first cow, during the first period, we give it a treatment or diet and we measure the yield. Obviously, you don't have any carryover effects here because it is the first period. However, what if the treatment they were first given was a really bad treatment?
9 - Randomized Block Design: Two-way MANOVA
Statology is a site that makes learning statistics easy by explaining topics in simple and straightforward ways. Our team of writers have over 40 years of experience in the fields of Machine Learning, AI and Statistics. You can obtain the 'least squares means' from the estimated parameters from the least squares fit of the model. My guess is that they all started the experiment at the same time - in this case, the first model would have been appropriate. Let's take a look at how this is implemented in Minitab using GLM. Use the viewlet below to walk through an initial analysis of the data (cow_diets.mwx | cow_diets.csv) for this experiment with cow diets.
ANOVA: Yield versus Batch, Pressure
The Analysis of Variance table shows three degrees of freedom for Tip three for Coupon, and the error degrees of freedom is nine. In this experiment, each specimen is called a “block”; thus, we have designed a more homogenous set of experimental units on which to test the tips. Interpretation of the coefficients of the corresponding models, residualanalysis, etc. is done “as usual.” The only difference is that we do not test theblock factor for statistical significance, but for efficiency. Instead of a single treatment factor, we can also have a factorial treatmentstructure within every block. We use the usual aov function with a model including the two main effectsblock and variety.
Identify nuisance variables
To do a crossover design, each subject receives each treatment at one time in some order. So, one of its benefits is that you can use each subject as its own control, either as a paired experiment or as a randomized block experiment, the subject serves as a block factor. It is just a question about what order you give the treatments. The smallest crossover design which allows you to have each treatment occurring in each period would be a single Latin square.
The selection of blocking variables should be based on previous literature. Randomized block design still uses ANOVA analysis, called randomized block ANOVA. When participants are placed into a block, we anticipate them to be homogeneous on the control variable, or the blocking variable. In other words, there should be less variability within each block on the control variable, compared to the variability in the entire sample if there were no control variable. Less within-block variability reduces the error term and makes estimate of the treatment effect more robust or efficient, compared to without the blocking variable.
A Case 3 approach involves estimating separate period effects within each square. To achieve replicates, this design could be replicated several times. Here is a plot of the least squares means for Yield with the missing data, not very different. There are 23 degrees of freedom total here so this is based on the full set of 24 observations. My mission is to empower the next generation of online entrepreneurs with the knowledge and tools they need to succeed.
We could select the first three columns - let's see if this will work. Click the animation below to see whether using the first three columns would give us combinations of treatments where treatment pairs are not repeated. Is the period effect in the first square the same as the period effect in the second square?
Use the animation below to see how this example of a typical treatment schedule pans out. When the data are complete this analysis from GLM is correct and equivalent to the results from the two-way command in Minitab. What if the missing data point were from a very high measuring block? It would reduce the overall effect of that treatment, and the estimated treatment mean would be biased.
Each batch of resin is called a “block”, since a batch is a more homogenous set of experimental units on which to test the extrusion pressures. Below is a table which provides percentages of those products that met the specifications. In studies involving human subjects, we often use gender and age classes as the blocking factors. We could simply divide our subjects into age classes, however this does not consider gender. Therefore we partition our subjects by gender and from there into age classes. Thus we have a block of subjects that is defined by the combination of factors, gender and age class.

No comments:
Post a Comment